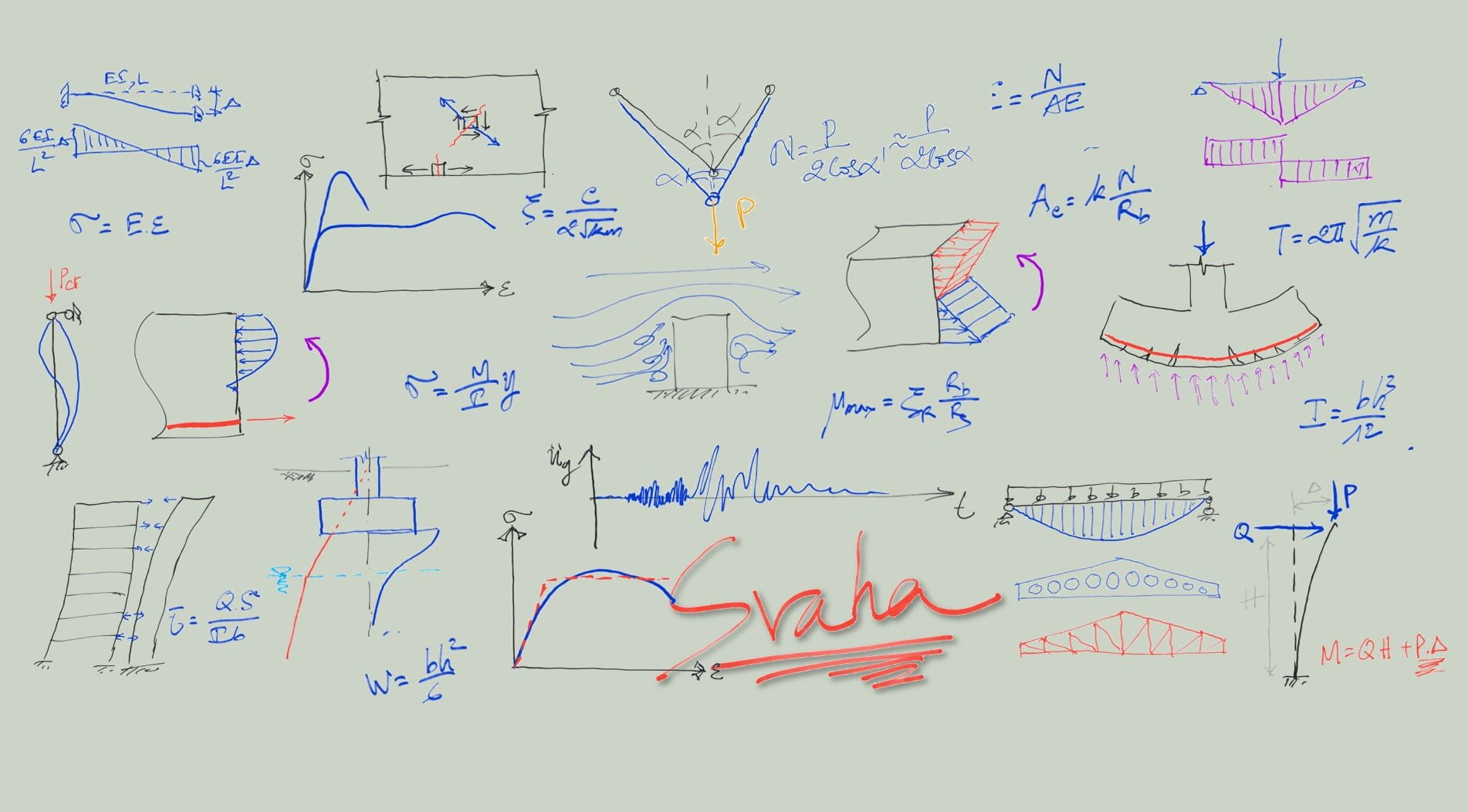
Trên hình vẽ dưới đây, véc tơ lực \(F_u\) và \(F_v\) có chung gốc và xác định nên hình bình hành \(ABCD\). Véc tơ lực \(F\) là đường chéo của hình bình hành, có gốc trùng với gốc của \(F_u\) và \(F_v\). Khi đó ta nói lực \(F\) tương đương với hệ gồm hai lực \(F_u\) và \(F_v\). Nghĩa là nếu thay thế lực \(F_u\) và \(F_v\) bằng lực \(F\) thì tác dụng không thay đổi. Ngược lại, nếu thay thế lực \(F\) bằng lực \(F_u\) và \(F_v\) thì tác dụng cũng không thay đổi. Đây gọi là quy tắc hình bình hành lực.
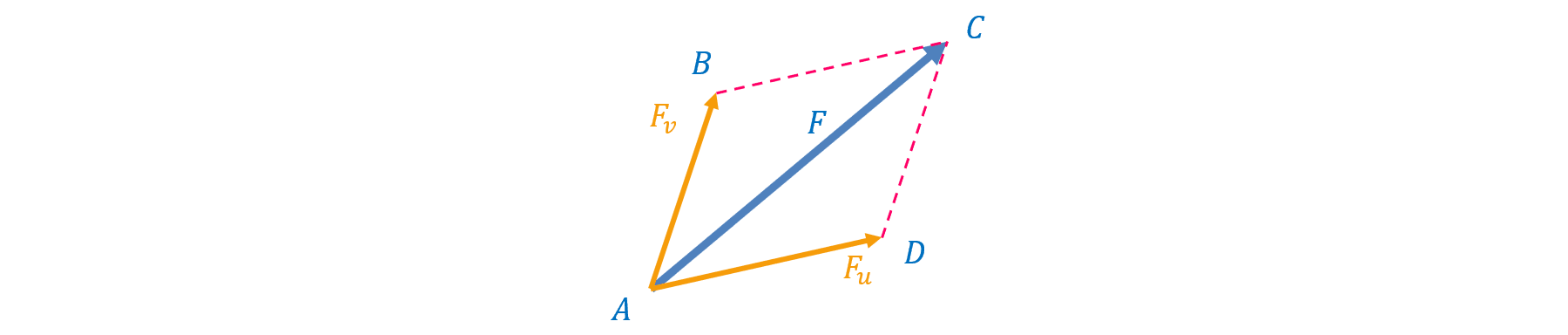
Trong thực tế áp dụng, ta thường sử dụng quy tắc hình bình lực trên đây để phân tích véc tơ lực \(F\) lên hai phương vuông góc, thường là phương ngang và phương đứng, như hình dưới đây. Lưu ý rằng ở đây ta đã sử dụng quy tắc hình bình hành lực để phân tích lực \(F\) thành hai lực vuông góc nhau \(F_x\) và \(F_y\) chứ không phải là chiếu véc tơ lực\(F\) lên phương \(x\) và phương \(y\).
Ví dụ
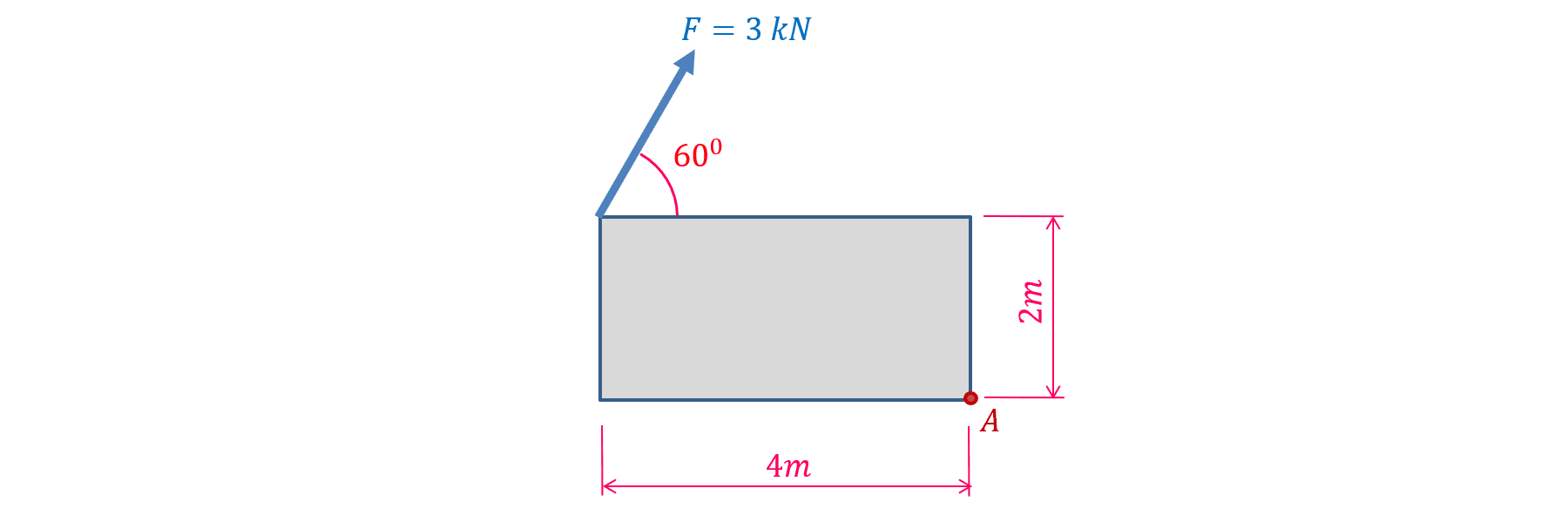
Xác định mô men của lực \(F\) đối với điểm \(A\) trên hình dưới đây.
(xem thêm: mô men của một lực đối với một điểm)
Bài giải:
Ta có thể tính trực tiếp mô men của lực \(F\) đối với điểm \(A\) bằng cách xác định cánh tay đòn của nó rồi tính giá trị và xác định chiều xoay của mô men.
Tuy nhiên, việc làm như vậy có thể phức tạp về mặt hình học ở bước xác định chiều dài của cánh tay đòn. Vì vậy ta sẽ áp dụng quy tắc hình bình hành lực để tính mô men như sau:
Phân tích lực \(F\) lên phương ngang và phương đứng, ta sẽ được các lực màu đỏ như hình dưới đây (tham khảo hệ thức lượng trong tam giác vuông để biết cách tính giá trị của các thành phần này). Khi đó ta có hệ lực màu đỏ tương đương với lực màu xanh. Như vậy thay vì tính mô men của lực màu xanh thì ta tính mô men của hai lực màu đỏ.
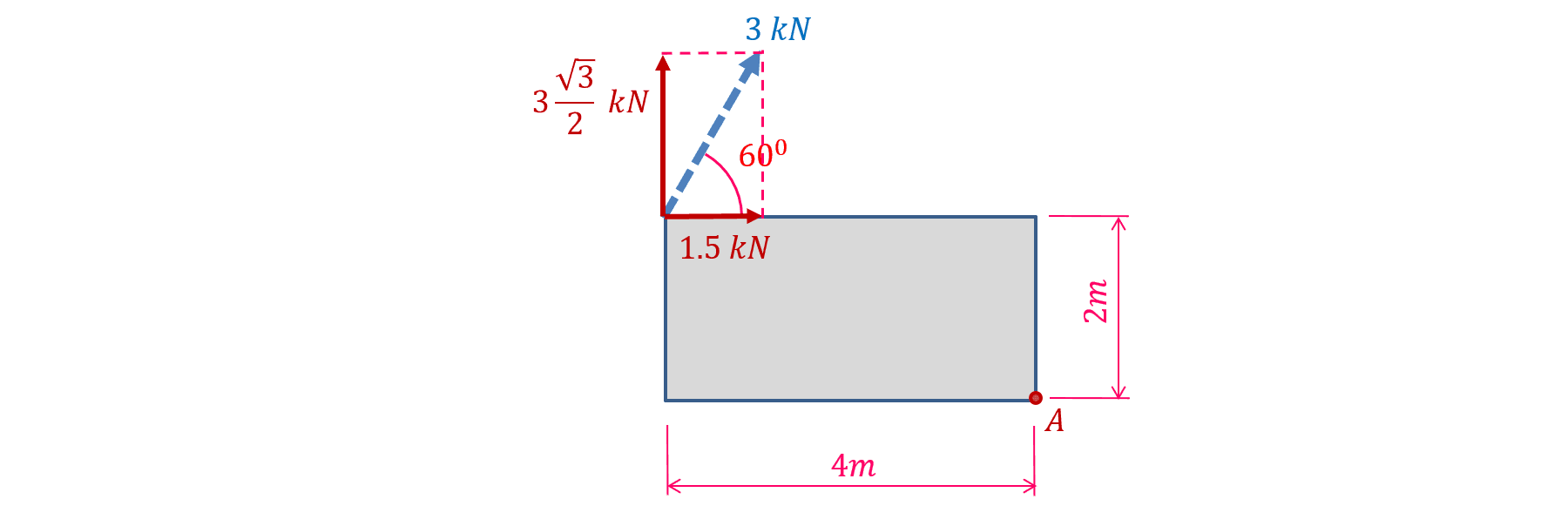
Giải sử mô men xoay thuận chiều kim đồng hồ là dương, ta có mô men của hệ lực màu đỏ đối với điểm \(A\) là:
\(M=1.5\times 2 +3\frac{\sqrt{3}}{2}\times 4 = 3(2\sqrt{3}+1) (kNm)\)
Giá trị mô men tính ra là dương nên mô men này xoay thuận chiều kim đồng hồ (theo giả sử bên trên).