Back to: CƠ HỌC CÔNG TRÌNH
Trọng tâm bài học
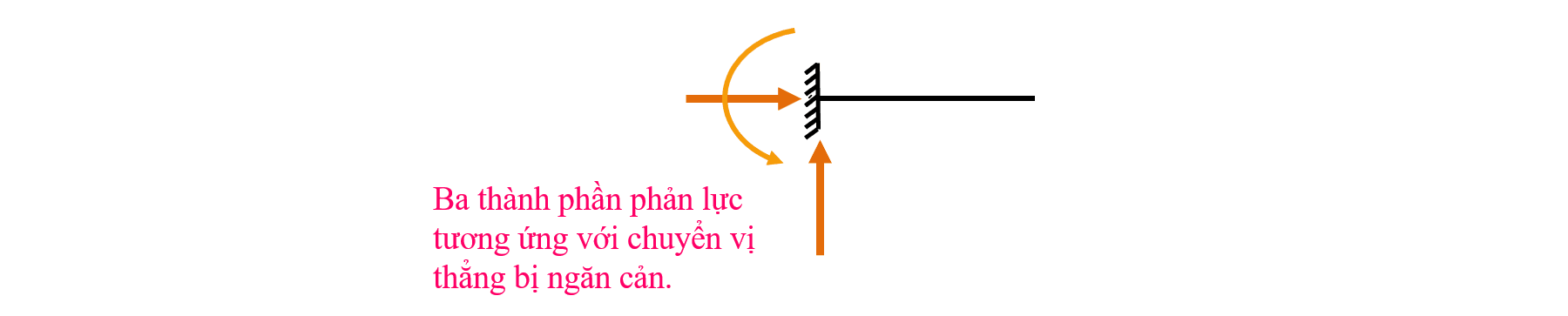
Gối tựa ngàm dùng để ngăn cản cả 3 thành phần chuyển vị tại một tiết diện thanh. Khi đó trong liên kết ngàm xuất hiện ba thành phần phản lực, gồm hai thành phần lực và một thành phần mô men (xem hình dưới đây). Chú ý rằng hai thành phần lực có thể theo hai phương bất kỳ (miễn là hai phương này không trùng nhau) nhưng trong tính toán người ta thường sử dụng thành phần nằm ngang và thẳng đứng.
Ví dụ
Xác định các thành phần phản lực tại ngàm \(A\) của hệ chịu lực như hình dưới đây:
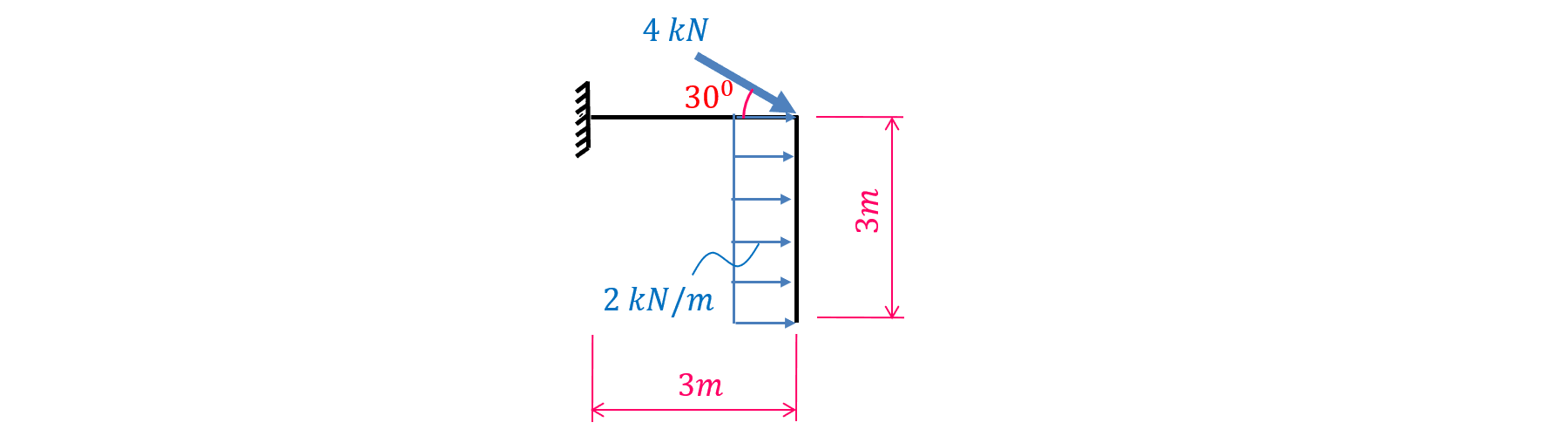
Bạn có thể tham khảo thêm về: Hợp lực của lực phân bố; Mô men của một lực đối với một điểm; Phương trình cân bằng lực; Phương trình cân bằng mô men.
Bài giải:
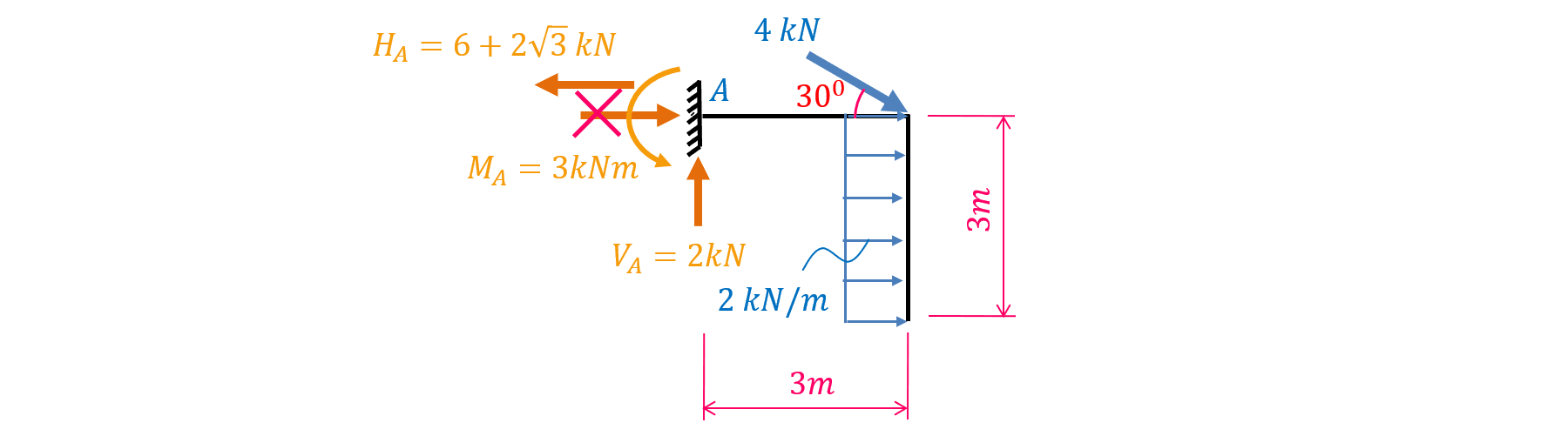
Vì \(A\) là gối tựa ngàm nên tại đó xuất hiện 3 thành phần phản lực. Gọi các thành phần phản lực là \(H_A\), \(V_A\) và \(M_A\) như hình dưới đây (\(H\) là viết tắt của từ Horizontal, \(V\) là viết tắt của từ Vertical).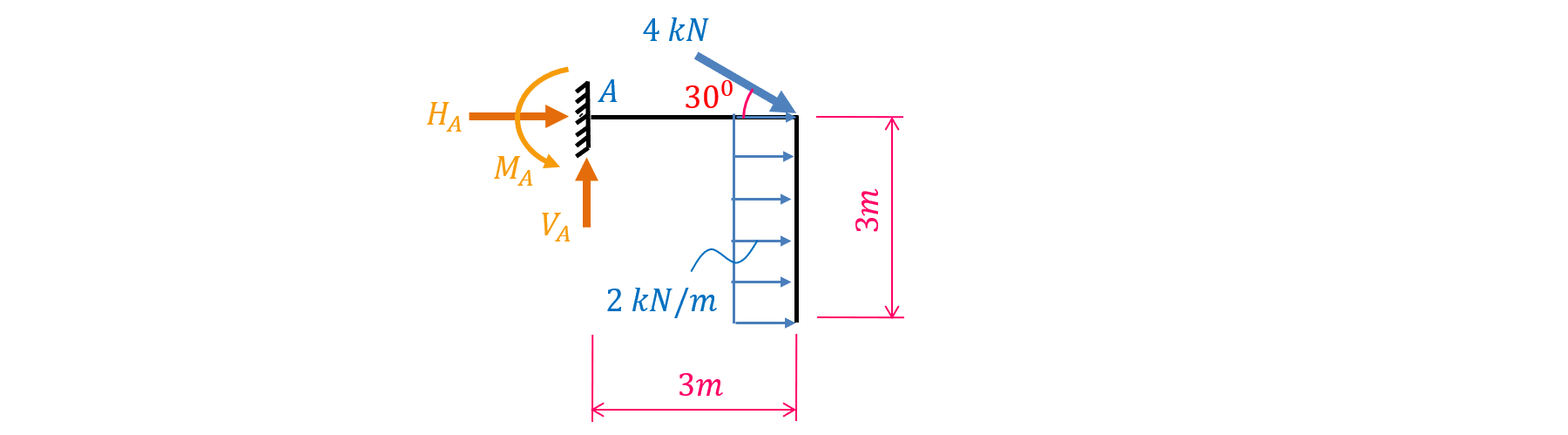
Để tìm các phản lực \(V_A\), \(H_A\) và \(M_A\), ta sử dụng nguyên tắc: muốn tìm một lực chưa biết trong số 3 lực phẳng không đồng quy, không song song, ta sử dụng phương trình cân bằng sao cho có thể loại bỏ được hai lực còn lại (xem thêm bài Ví dụ 2 tại đây).
Để tính \(H_A\), ta sử dụng phương trình cân bằng không chứa \(V_A\) và \(M_A\). Muốn loại bỏ \(M_A\) thì ta không thể sử dụng phương trình cân bằng mô men được (vì \(M_A\) là mô men tập trung nên lấy mô men tại điểm nào nó cũng tham gia, xem thêm tại đây). Như vậy ở đây ta sẽ sử dụng phương trình cân bằng lực. Khi sử dụng phương trình cân bằng lực thì \(M_A\) sẽ không tham gia (xem thêm tại đây). Lúc này ta chỉ cần quan tâm là sử dụng phương trình cân bằng lực nào để loại bỏ \(V_A\) mà thôi. Phương trình cân bằng lực có thể loại bỏ được \(V_A\) là phương trình cân bằng theo phương ngang (là phương vuông góc với \(V_A\)).
Phương trình cân bằng lực theo phương ngang (giả thiết chiều dương hướng sang phải) được viết là:
\(H_A+4\times cos30^{0 (*)}+ 2\times 3 ^{(**)}= 0\)
(\(^{(*)}\): xem thêm tại đây; \(^{(**)}\): xem thêm tại đây)
Suy ra \(H_A = -(6+2\sqrt{3}) (kN)\).
Lập luận tương tự như trên, để tính \(V_A\) thì ta sử dụng phương trình cân bằng lực theo phương đứng. Kết quả là \(V_A=2 kN\).
Để tính mô men \(M_A\) thì ta sử dụng phương trình cân bằng sao cho có thể loại bỏ được \(H_A\) và \(V_A\). Muốn vậy thì ta sử dụng phương trình cân bằng mô men tại điểm \(A\), là giao điểm của \(H_A\) và \(V_A\).
Quy ước mô men xoay theo chiều kim đồng hồ là dương (xem cách xác định chiều xoay của mô men tại đây), phương trình cân bằng mô men tại điểm \(A\) có dạng:
\(-M_A^{(*)} +4\times 3\times sin30^{0 (**)} – 2\times 3\times 1.5 ^ {(***)}= 0\)
(\(^{(*)}\): xem thêm tại đây; \(^{(**)}\): xem thêm tại đây; \(^{(***)}\): xem thêm tại đây)
Suy ra \(M_A=3 (kNm)\)
Ở đây ta tính ra \(H_A\) âm. Điều này có nghĩa là chiều của \(H_A\) là ngược lại của chiều giả thiết trên đây. Để thuận lợi cho các tính toán về sau, ta đánh chéo chiều giả thiết của \(H_A\) (không xóa) rồi vẽ chiều thực cùng giá trị của nó như hình vẽ dưới đây: