Phương trình của hàm bậc hai có dạng:
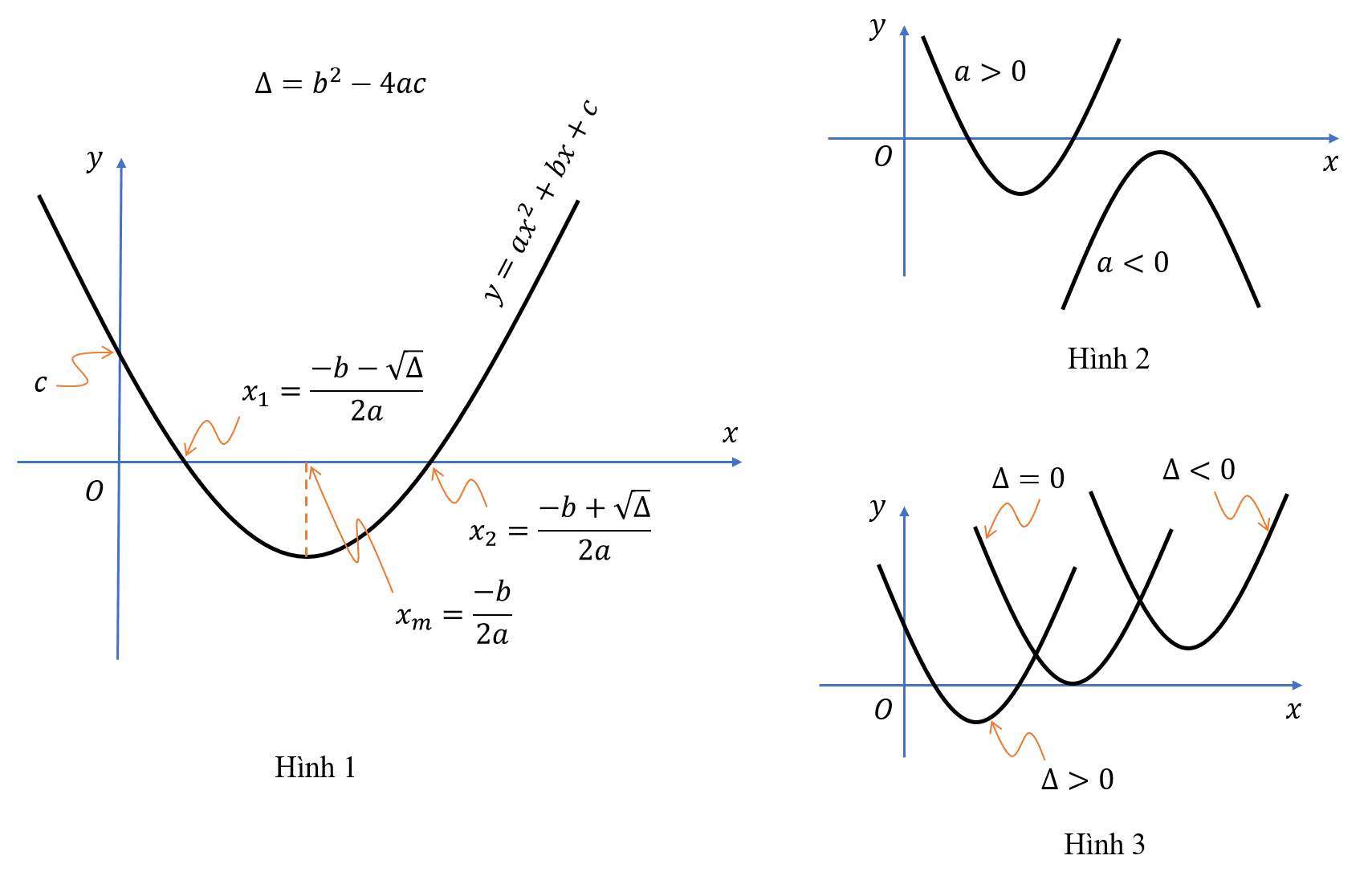
\(y = ax^2 + bx + c\) với \(a \neq 0\)
Đồ thị của nó là một parabola như các hình trên. Nếu \(a>0\) thì đồ thị của nó là lõm, nếu \(a<0\) thì đồ thị là lồi như trên Hình 2.
Đồ thị đạt cực trị tại hoành độ \(x_m = -\frac{b}{2a}\)
Đặt:
\(\Delta = b^2 – 4ac\)
Nếu \(\Delta > 0\) thì đồ thị cắt trục hoành tại hai điểm có hoành độ là \(x_1\) và \(x_2\) như trên Hình 1. Hai hoành độ này cũng chính là nghiệm của phương trình \(ax^2 + bx + c = 0\).
Nếu \(\Delta = 0\) thì đồ thị tiếp xúc với trục hoành tại điểm có hoành độ \(x_m\). Giá trị \(x_m\) này chính là nghiệm kép của phương trình \(ax^2 + bx + c = 0\).
Nếu \(\Delta < 0\) thì đồ thị không cắt trục hoành. Khi đó phương trình \(ax^2 + bx + c = 0\) vô nghiệm.