Đối với một hệ lực cân bằng thì tổng đại số (tức là có lấy dấu) của hình chiếu tất cả các lực lên một hướng nào đó phải bằng \(0\).
Ví dụ áp dụng:
Xác định giá trị của các lực \(X_1\), \(X_2\) để hệ lực trong hình dưới đây cân bằng.
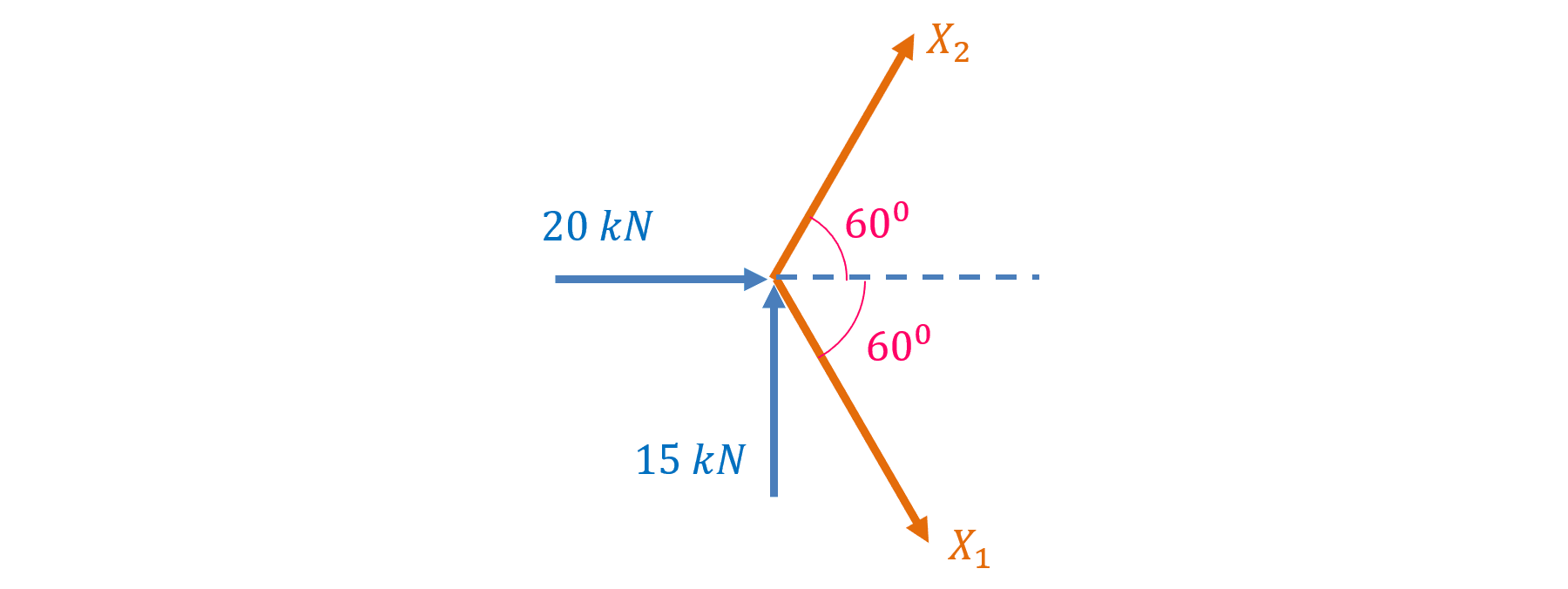
Cách tiếp cận 1:
Để hệ lực trên cân bằng thì tổng đại số hình chiếu tất cả các lực lên phương ngang phải bằng \(0\). Nghĩa là:
\(X_1 cos60^o + X_2 cos 60^o + 20 = 0\) (1)
Để hệ lực trên cân bằng thì tổng đại số hình chiếu tất cả các lực lên phương đứng phải bằng \(0\). Nghĩa là:
\(-X_1 sin60^o + X_2 sin 60^o + 15 = 0\) (2)
(chú ý ở đây ta lấy tổng đại số nên phải lấy dấu của véc tơ hình chiếu)
Giải hệ phương trình (1) và (2) ta được:
\(X_1 = -(20-5\sqrt{3}) (kN); X_2 = -(20+5\sqrt{3}) (kN)\)
Dấu “\(-\)” ở đây để chỉ rằng các lực \(X_1\), \(X_2\) có chiều ngược lại so với chiều trong hình vẽ bên trên. Nghĩa là hệ lực cân bằng được cho như hình dưới đây:
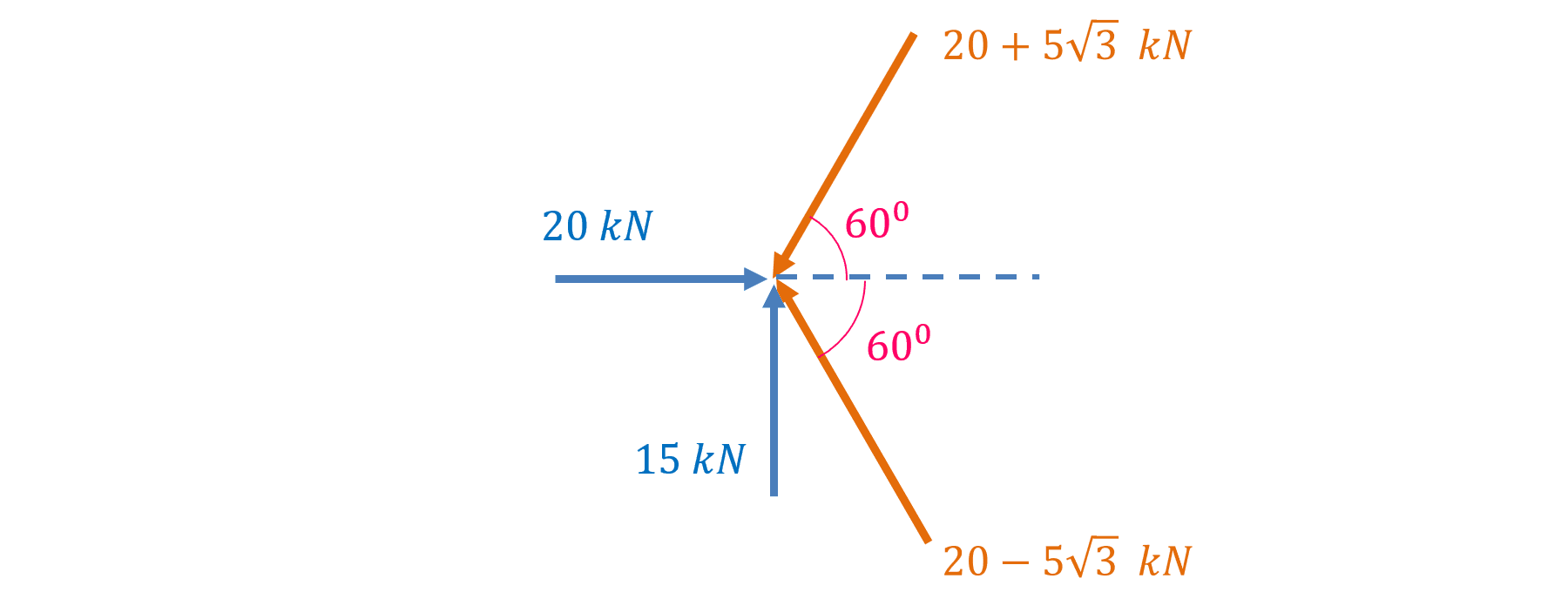
Cách tiếp cận 2:
Trong cách tiếp cận này, để tìm một lực nào đó, ta viết phương trình cân bằng sao cho có thể triệt tiêu được các lực chưa biết khác. Cụ thể, nếu ta muốn tìm lực \(X_1\) thì ta chiếu tất cả các lực lên hướng vuông góc với lực \(X_2\) (ở đây là hướng của trục \(u\) ) như hình bên dưới:
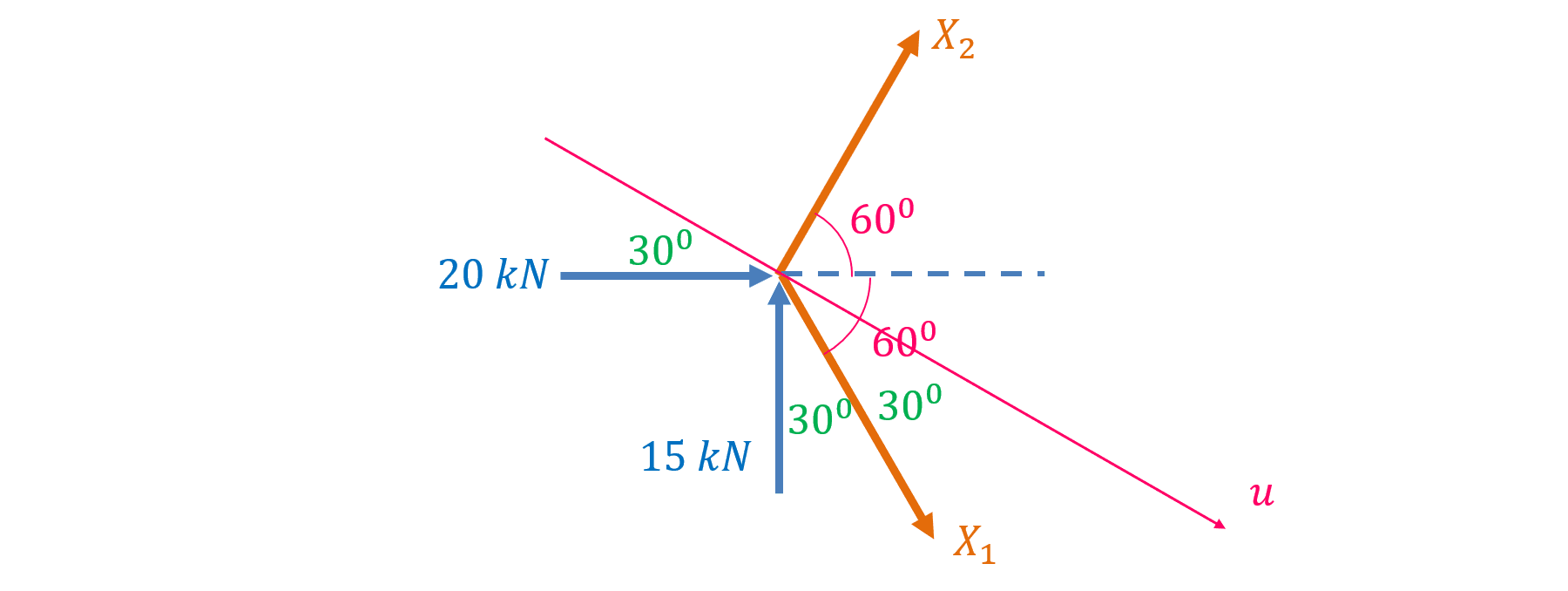
Phương trình hình chiếu của tất cả các lực lên hướng \(u\) là:
\(X_1 cos30^o – 15 cos60^o + 20 cos30^o = 0\)
Thay \(cos30^o = \sqrt{3}/2; cos60^o = 1/2\) vào phương trình trên ta được \(X_1=-(20-5\sqrt{3}) (kN)\).
Tương tự như vậy, nếu muốn tìm lực \(X_2\) thì ta chiếu hệ lực lên hướng \(v\) vuông góc với lực \(X_1\) như hình dưới đây:
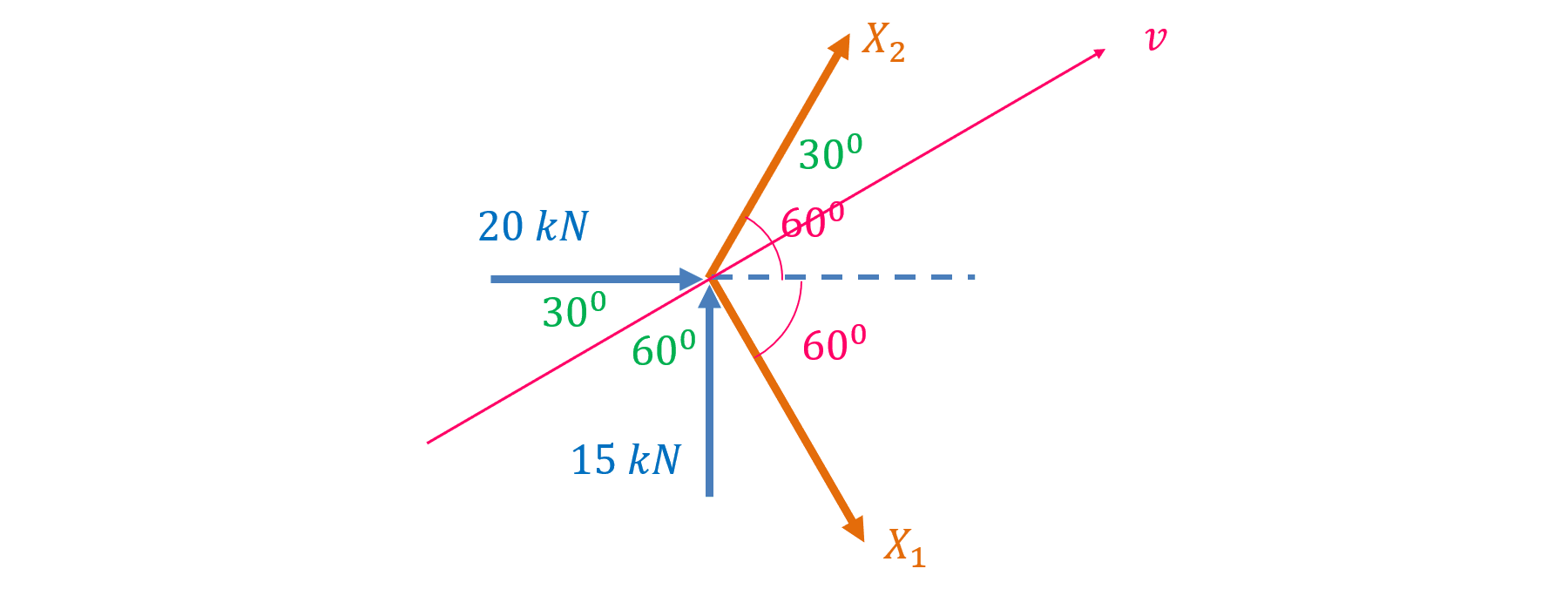
Phương trình hình chiếu tất cả các lực lên phương \(v\) là:
\(X_2 cos30^0 + 20 cos30^o + 15 cos 60^o = 0\)
Thay \(cos30^o = \sqrt{3}/2; cos60^o = 1/2\) vào phương trình trên ta được \(X_2=-(20+5\sqrt{3}) (kN)\) .