Cho tam giác vuông có độ dài các cạnh là \(a\), \(b\), \(c\), có các góc nhọn là \(\alpha\), \(\beta\) như hình vẽ dưới đây.
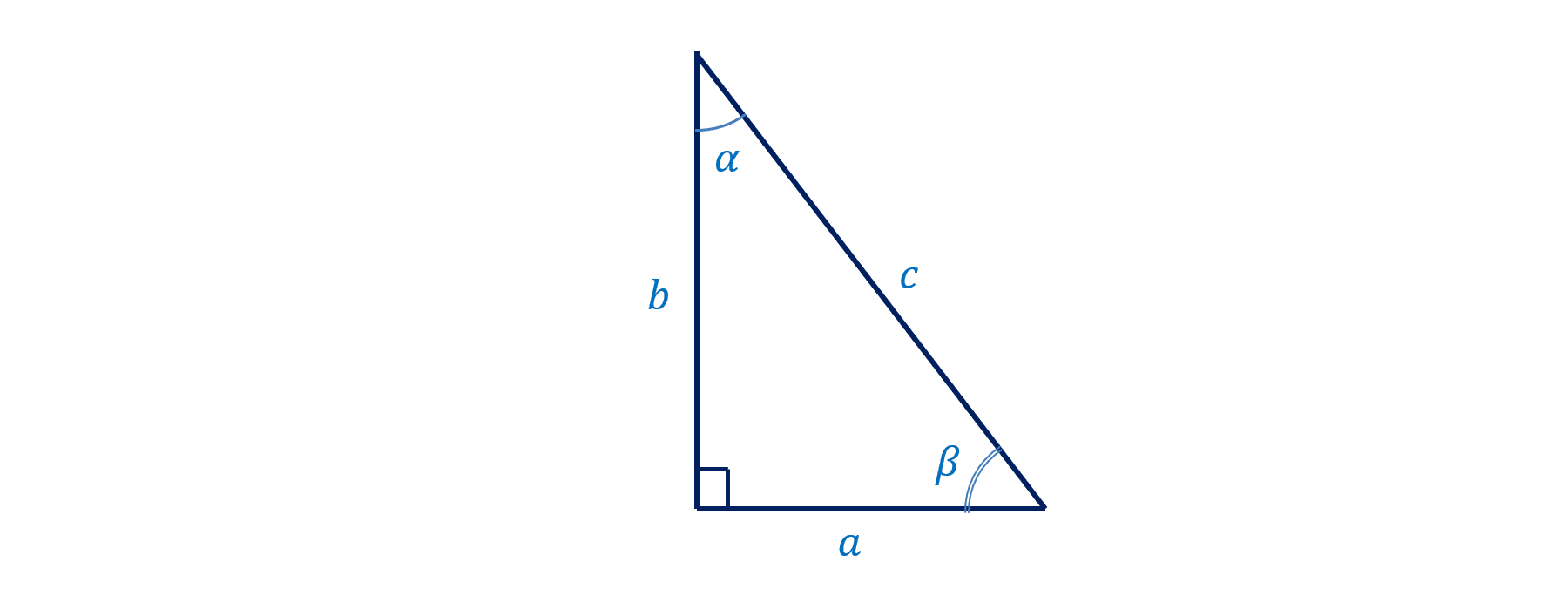
Khi đó ta có quan hệ giữa các góc và các cạnh của tam giác vuông như sau:
\(sin\alpha = \frac{a}{c}; cos\alpha = \frac{b}{c}; tan\alpha = \frac{a}{b}\)
\(sin\beta = \frac{b}{c}; cos\beta = \frac{a}{c}; tan\beta = \frac{b}{a}\)
Hồi nhỏ nhớ có học bài thơ sau (hình như trong sách của tác giả Võ Đại Mau thì phải — không nhớ rõ lắm):
Tìm sin lấy đối chia huyền,
cosin hai cạnh kề huyền chia nhau,
Còn tan ta sẽ tính mau,
Đối trên kề dưới chia nhau sẽ thành.
Chú ý là cạnh \(a\) là cạnh đối (đối diện) của góc \(\alpha\), còn cạnh \(b\) là cạnh kề (ngay sát nách) của góc \(\alpha\).
Theo quan hệ trên, ta có:
\(a=c\times cos\beta; a = c\times sin\alpha\)
Nghĩa là: cạnh góc vuông bằng cạnh huyền nhân sin góc đối hoặc nhân cos góc kề.
Theo tiếng Việt của Công Nghệ Giáo Dục thì âm k và âm c đều phát âm giống nhau là cờ. Như vậy kề đi đôi với cos (cùng có âm cờ), cứ hễ cos là kề. Dễ nhớ nhỉ.