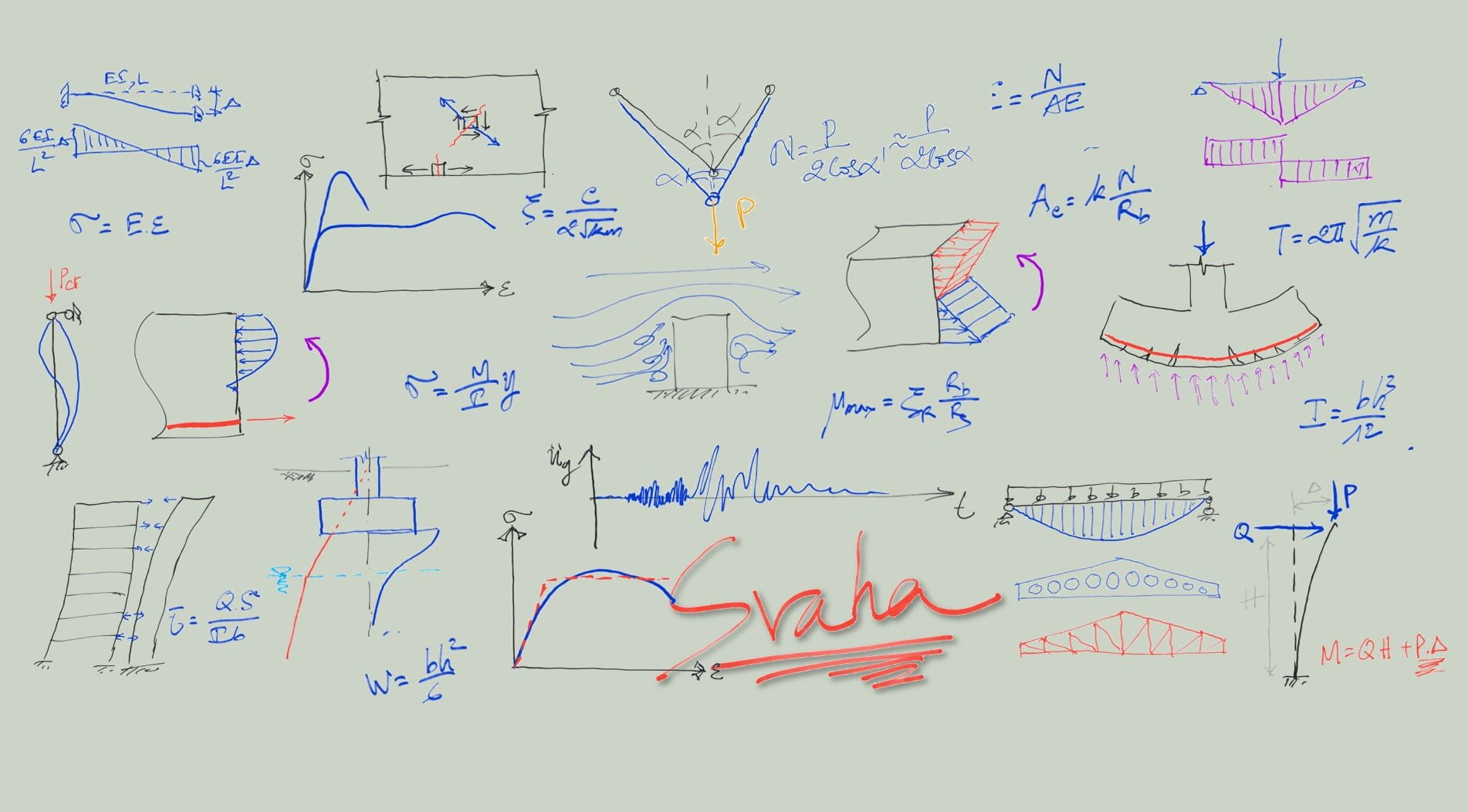
Trong hình dưới đây, \(R\) là hợp lực của hệ lực phân bố \(q\). Khi đó giá trị của \(R\) và vị trí của nó được xác định như công thức bên cạnh.
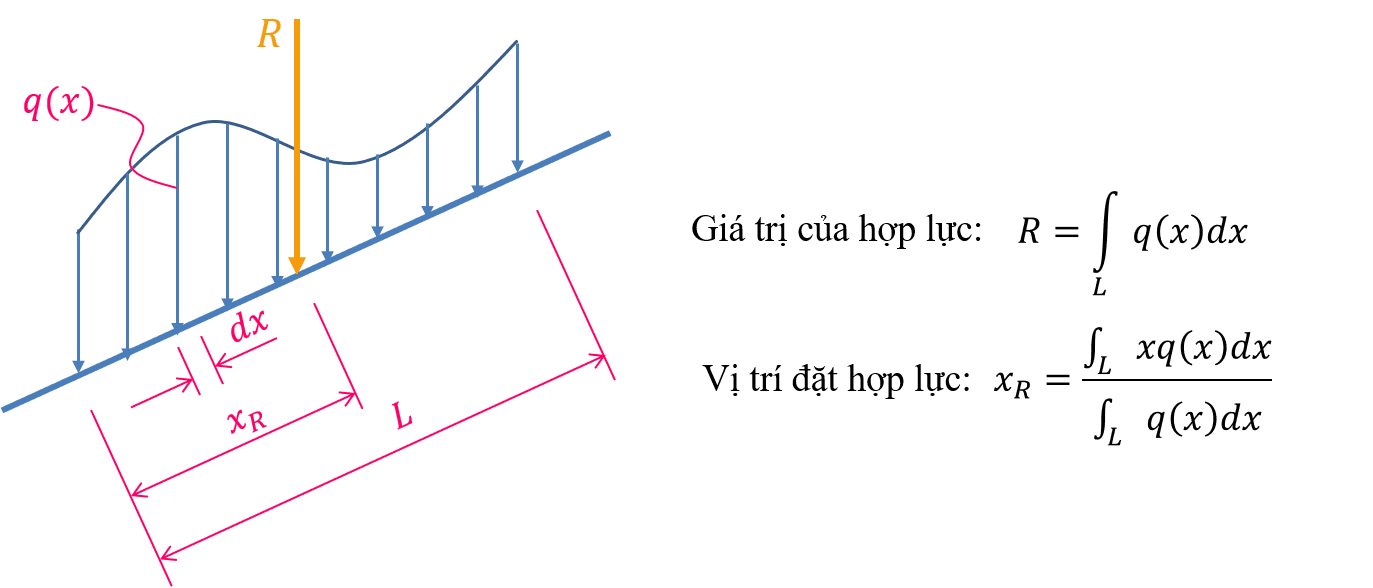
Hình dưới đây biểu diễn hợp lực của một số dạng tải phân bố thường gặp:
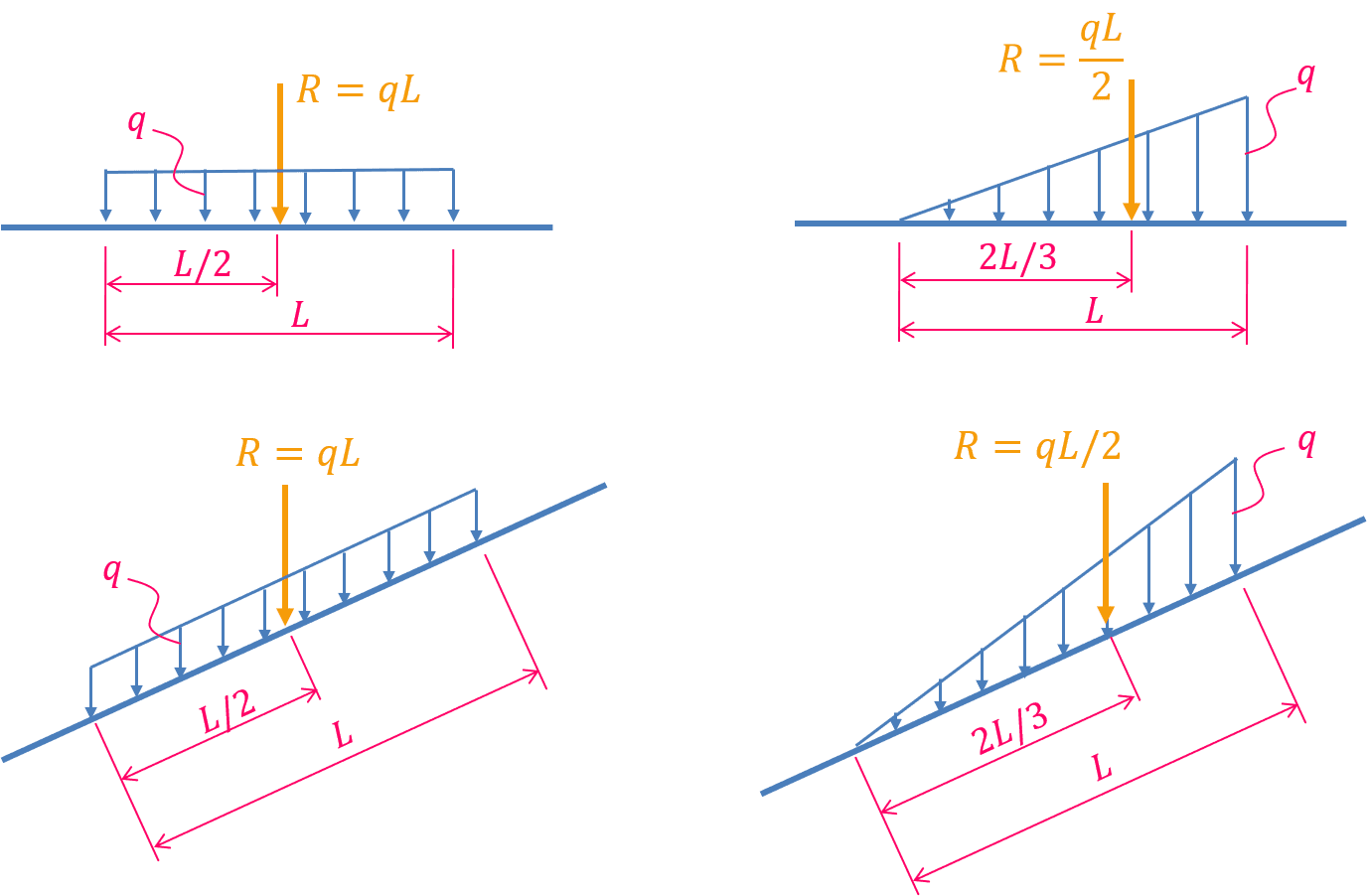
Ví dụ áp dụng 1
Tính mô men của hệ lực phân bố trên hình sau đối với điểm A.

Bài giải:
Thay vì đi tính trực tiếp mô men của hệ lực phân bố tam giác đối với điểm A, ta đi tính mô men của hợp lực của nó đối với điểm A.
Hợp lực của lực phân bố trên đây có giá trị là \(P=\frac{1}{2}\times 20\times 6=60 (kN)\). Hợp lực này đặt cách đầu mút bên trái một đoạn bằng \(\frac{2}{3}\times 6 = 4 (m)\). Nghĩa là cánh tay đòn của hợp lực đối với điểm \(A\) là \(2 + 4 = 6 (m)\).
Như vậy mô men của lực phân bố đối với điểm \(A\) là \(M=60\times 6 = 360 (kNm)\). Mô men này xoay ngược chiều kim đồng hồ (xem lại cách xác định chiều xoay của mô men tại đây).
Ví dụ áp dụng 2
Tính mô men của hệ lực sau đối với điểm \(A\):
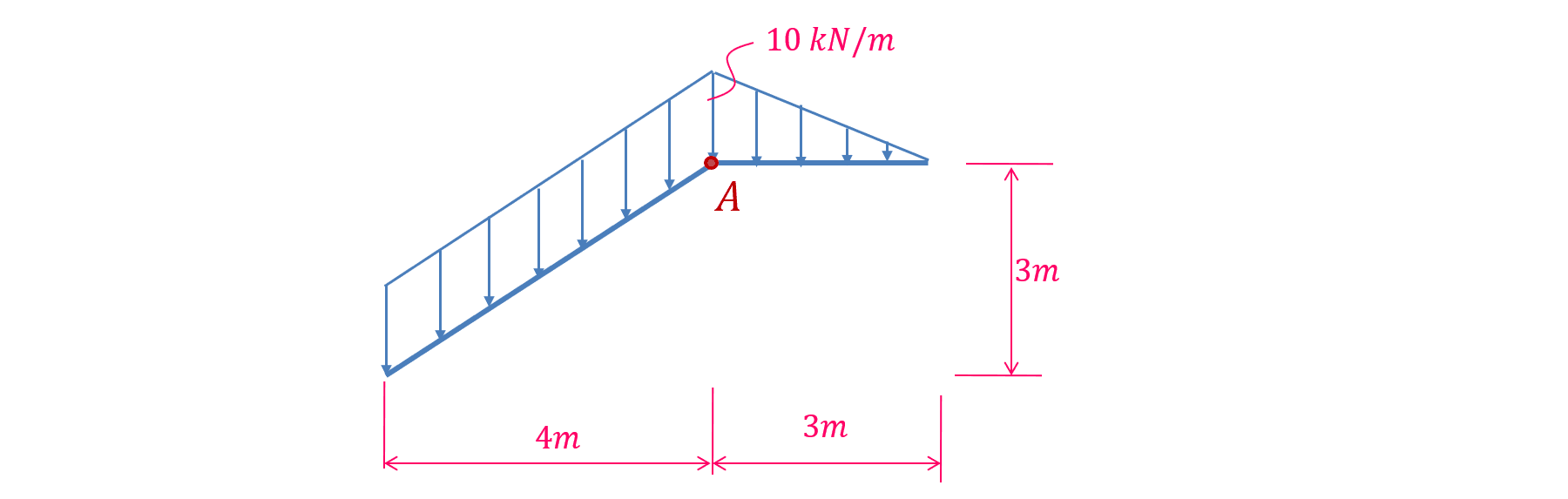
Bài giải:
Theo định lý Pythagoras, Chiều dài của thanh xiên là \(5m\).
Giả sử mô men xoay thuận chiều kim đồng hồ là dương. Mô men của hệ lực trên đối với điểm \(A\) được tính là:
\(M=-(10 kN/m\times 5 m)\times 2m + \frac{1}{2}\times10 kN/m\times 3\times 1 m=-85 kNm\)
Dấu “-” ở đây chỉ rằng mô men này là xoay ngược chiều kim đồng hồ.
Trong biểu thức trên, số hạng đầu tiên là mô men của hệ lực phân bố đều tác dụng trên thanh xiên, số hạng thứ hai là mô men của hệ lực phân bố tam giác tác dụng trên thanh ngang.